مقاييس التشتت في الإحصاء
في مجال الإحصاء، يعد فهم مقاييس التشتت من الأساسيات المهمة التي تساعد في تفسير البيانات بشكل دقيق، بينما تركز المقاييس المركزية مثل المتوسط أو الوسيط على تقديم قيمة تمثل مركز البيانات، فإن مقاييس التشتت تهدف إلى قياس مدى تباين أو تشتت البيانات حول تلك القيمة المركزية، بمعنى آخر، تقدم مقاييس التشتت في الإحصاء فكرة عن انتشار البيانات ومدى تباينها، وهو ما يساعد الباحثين والمحللين في فهم مدى تنوع النتائج التي تم جمعها.
في هذه المقالة، سنتعرف على مقاييس التشتت في الإحصاء، أنواعها المختلفة، وكيفية استخدام هذه المقاييس في تحليل البيانات الإحصائية.
جدول المحتويات
ما هي مقاييس التشتت في الإحصاء؟
مقاييس التشتت هي أدوات إحصائية تستخدم لتحديد مدى التباين أو انتشار البيانات عن المتوسط أو القيمة المركزية لمجموعة البيانات، فكلما كان التشتت أكبر، كانت القيم بعيدة عن المتوسط، مما يشير إلى تنوع أكبر في البيانات، أما إذا كان التشتت صغيرًا، فهذا يعني أن معظم القيم قريبة من المتوسط.
يمكن لمقاييس التشتت أن تساعد في تحديد ما إذا كانت البيانات متمركزة حول نقطة معينة أو ما إذا كانت موزعة بشكل واسع، فهي ضرورية لفهم وتحليل المتغيرات في البيانات واستخلاص الاستنتاجات الصحيحة منها.
أهمية مقاييس التشتت
مقاييس التشتت مهمة في الإحصاء لعدة أسباب، منها:
- التنبؤ بالأنماط المستقبلية: من خلال معرفة تشتت البيانات، يتم التنبؤ بما قد يحدث في المستقبل أو كيفية تصرف البيانات في المستقبل.
- فهم دقة المتوسط: على الرغم من أن المتوسط يُعطي فكرة عن “مركز” البيانات، فإن مقاييس التشتت تساهم في توضيح مدى دقة هذا المتوسط.
- تحليل التنوع: تساعد مقاييس التشتت في فهم مدى التوزيع والاختلاف بين القيم في البيانات.
أنواع مقاييس التشتت
هناك عدة أنواع من مقاييس التشتت التي تستخدم في الإحصاء، وأشهر هذه المقاييس هي:
1- المدى (Range)
المدى هو أبسط مقياس للتشتت، وهو يعبر عن الفارق بين أعلى قيمة وأدنى قيمة في مجموعة البيانات، ويتم حسابه باستخدام المعادلة التالية:
- المدى= أعلى قيمة − أدنى قيمة
مزايا المدى:
- سهل الحساب ولا يتطلب معلومات إضافية.
- يعطي فكرة عامة عن مدى انتشار البيانات.
عيوب المدى:
- الحساسية للقيم المتطرفة: إذا كان هناك قيمة شاذة أو متطرفة (outlier)، فإنها تؤثر بشكل كبير على المدى.
2- الانحراف المعياري (Standard Deviation)
الانحراف المعياري من مقاييس التشتت في الإحصاء التي تظهر التشتت حول المتوسط ويعتبر من أهم المقاييس المستخدمة في الإحصاء، ويعبر الانحراف المعياري عن متوسط الابتعاد للقيم عن المتوسط، ويُحسب باستخدام المعادلة التالية:

حيث:
- xix_i هي القيم الفردية في مجموعة البيانات.
- μ\mu هو المتوسط.
- nn هو عدد القيم في البيانات.
مزايا الانحراف المعياري:
- يُعطي فكرة دقيقة عن مدى انتشار البيانات.
- يستخدم في التحليل الاحصائي بكثرة، وخاصة في دراسات التوزيع الطبيعي.
عيوب الانحراف المعياري:
- الحساسية للقيم المتطرفة: مثل المدى، يتأثر الانحراف المعياري بالقيم المتطرفة بشكل كبير.
3- التباين (Variance)
التباين هو مقياس آخر للتشتت وهو عبارة عن مربع الانحراف المعياري، ويستخدم التباين بشكل رئيسي في التحليل الإحصائي والنمذجة الرياضية، حيث يساعد في دراسة التشتت على نطاق واسع، ويُحسب التباين باستخدام المعادلة التالية:
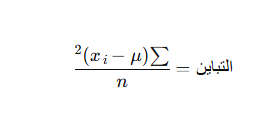
مزايا التباين:
- مفيد في العمليات الرياضية والتطبيقات التي تتطلب مقاييس رياضية دقيقة.
- يوفر مقياسًا دقيقًا عن انتشار البيانات.
عيوب التباين:
- يُظهر التباين وحدة قياس مربعة (أي المتر المربع أو الجرام المربع)، وهذا يجعله صعب الفهم في بعض الحالات.
4- معامل التشتت (Coefficient of Variation – CV)
معامل التشتت هو مقياس من مقاييس التشتت في الإحصاء وهو مق نسبية يستخدم الانحراف المعياري مقارنة بالمتوسط، ويستخدم هذا المقياس بشكل رئيسي في المقارنات بين مجموعات بيانات ذات وحدات مختلفة أو عندما يكون للبيانات نطاق واسع من القيم، ويحسب معامل التشتت باستخدام المعادلة التالية:
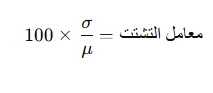
حيث:
- σ\sigma هو الانحراف المعياري.
- μ\mu هو المتوسط.
مزايا معامل التشتت:
- يمكن مقارنته عبر مجموعات بيانات متعددة أو عمليات صناعية مختلفة.
- يُعتبر مقياسًا مفيدًا في تقييم المخاطر أو التباين في الأعمال.
عيوب معامل التشتت:
- قد لا يكون دقيقًا إذا كانت البيانات تحتوي على قيم متطرفة.
5- الربيعات (Interquartile Range – IQR)
الربيعات هو مقياس يستخدم في دراسة التوزيع للتقليل من تأثير القيم المتطرفة، ويُحسب الربيع باستخدام الفارق بين الربيع الأول (Q1) والربيع الثالث (Q3)، وهو يوفر نطاقًا يشير إلى التشتت الذي يحدث في 50% من البيانات، والمعادلة هي:
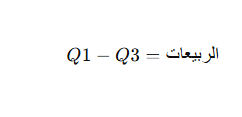
مزايا الربيعات:
- أقل حساسية للقيم المتطرفة مقارنة بالمدى أو الانحراف المعياري.
- يوفر مقياسًا دقيقًا للتشتت في البيانات اللامتناسقة.
عيوب الربيعات:
- قد لا يعطي رؤية كاملة في حالة وجود توزيع غير منتظم للبيانات.
استخدام مقاييس التشتت في البحث العلمي
مقاييس التشتت في الإحصاء أدوات أساسية لتحليل بيانات البحث العلمي، حيث تساهم في تحديد اتجاهات البيانات وتوفير معلومات حيوية حول مدى توزيع النتائج، ويمكن استخدام مقاييس التشتت في الإحصاء في العديد من المجالات البحثية مثل:
- الاقتصاد: لتحليل تباين الأسعار أو معدلات النمو الاقتصادي.
- الطب: لفحص فعالية العلاجات أو دراسة تباين المرضى.
- العلوم الاجتماعية: لدراسة التوزيع السكاني أو تأثير السياسات العامة.
- البحوث البيئية: لتقييم تغيرات درجات الحرارة أو مستوى التلوث.
مقاييس التشتت في الإحصاء هي أدوات مهمة لفهم البيانات بشكل أعمق، حيث تقدم صورة دقيقة عن كيفية توزيع البيانات ومدى تباينها، ومن خلال استخدام مقاييس مثل المدى، الانحراف المعياري، والتباين، يستخلص الباحثين والمحللين استنتاجات مفيدة تساعد في اتخاذ قرارات أفضل وتحقيق نتائج دقيقة.



